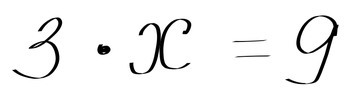
Итак, всё происходит из-за того, что существующие математические операции, строго говоря, неравноправны. "Вычитание" — по своей сути это сложение с отрицательным числом, "умножение" — это тоже сложение но некоторое количество раз числа с самим собой.

Но особенно выделяется среди математических операций "деление".
Все первичные абстрактные математические структуры, такие как перестановки, подстановки, группы и кольца как-то обходятся без деления. Но это уже совсем другая история.
Что такое деление ?
Давайте проследим за мыслью: что такое 9 : 3 ?
Первый вариант предполагает, что мы некие девять объектов раскладываем по трем кучкам.
Второй вариант — обратный. Он означает, что совместив предметы из трех кучек мы получим девять предметов. Это не что иное, как простейшее уравнение:

Здесь мы и подбираемся к моменту, когда начинаем понимать, почему нельзя делить на ноль. В действительности, любая запись, например, 7:0 эквивалентна уравнению:

Но мы же знаем, что при умножении любого числа на ноль ничего кроме нуля мы получить не можем, а значит и уравнение решений не имеет, а исходная запись бессмысленна.
А если делить 0 на 0 ?
А давайте зададимся вопросом, а можно ли НОЛЬ делить на ноль ? Ответ прост, сформулируем его в виде уравнения:

Чему тогда равен х, ведь подходит абсолютно любое число, какое бы мы не придумали. Т.е., другими словами, решение уравнения не определено, а деление нуля на ноль не имеет смысла.
А есть еще варианты?
Про выражение 0:0 говорят, что его невозможно вычислить непосредственно, но всё-таки можно вычислить методами математического анализа, если за 0 принимать некую "бесконечно малую" величину. Методы вычисления значения таких выражений в математики называются "раскрытием неопределенностей". В математике существует несколько видов определенностей:

Вот тут начинается настоящая "магия" для непосвященных: 0:0 может быть равен нулю, бесконечности или вообще обычному натуральному числу, а выражение "1 в степени бесконечность" вообще может снести крышу! Но именно в результате раскрытия такой неопределенности рождается знаменитое число Эйлера е=2,71828.
В момент знакомства с неопределенностями, я считаю, начинается настоящая математика!









